Problem: Invert a Binary Tree
leetcode.com/problems/invert-binary-tree/submissions/

Invert a binary tree.

Example:

Input:

     4
   /   \
  2     7
 / \   / \
1   3 6   9

Output:

     4
   /   \
  7     2
 / \   / \
9   6 3   1

​SOLUTION

The way I tend to remember it is: whenever we have to do something on the left and on the right, like merge sort and binary trees, break it down using recursion for the left and for the right first, then do the operation

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if root == None:
            return root
        if root.left == None and root.right == None:
            return root
        self.invertTree(root.left)
        self.invertTree(root.right)
        root.left, root.right = root.right, root.left
        return root

 
Binary Search Tree (BST)

https://leetcode.com/problems/search-in-a-binary-search-tree/

Given the root node of a binary search tree (BST) and a value. You need to find the node in the BST that the node's value equals the given value. Return the subtree rooted with that node. If such node doesn't exist, you should return NULL.

For example, 

Given the tree:
        4
       / \
      2   7
     / \
    1   3

And the value to search: 2

You should return this subtree:

      2     
     / \   
    1   3

In the example above, if we want to search the value 5, since there is no node with value 5, we should return NULL.

Note that an empty tree is represented by NULL, therefore you would see the expected output (serialized tree format) as [], not null.

​SOLUTION

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        if root == None or root.val == val:
            return root
        if val < root.val:
            return self.searchBST(root.left, val)
        if val > root.val:
            return self.searchBST(root.right, val)

Problem: Balance a Binary Search Tree

​leetcode.com/problems/balance-a-binary-search-tree/

Given a binary search tree, return a balanced binary search tree with the same node values.

A binary search tree is balanced if and only if the depth of the two subtrees of every node never differ by more than 1.

If there is more than one answer, return any of them.

 

Example 1:

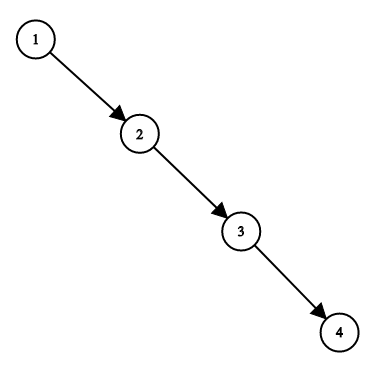
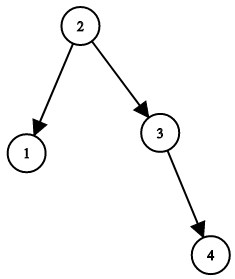
Input: root = [1,null,2,null,3,null,4,null,null]
Output: [2,1,3,null,null,null,4]
Explanation: This is not the only correct answer, [3,1,4,null,2,null,null] is also correct.

 

Constraints:

• The number of nodes in the tree is between 1 and 10^4.
• The tree nodes will have distinct values between 1 and 10^5.

SOLUTION:
* traverse the tree and store the elements into array O(n)
* Sort the array n log(n)
* Build a tree by recursive divide and conquer technique

Pay close attention to edge cases (2 element array)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
def store_to_array(root, arr):
    if root == None:
        return
    arr.append(root.val)
    store_to_array(root.left, arr)
    store_to_array(root.right, arr)
    
def build_a_tree(arr):
    if arr == None:
        return None
    if len(arr) == 1:
        return TreeNode(arr[0])
    mid = len(arr)//2
     
    root = TreeNode(arr[mid],\
                    build_a_tree(arr[:mid]),\
                    build_a_tree(arr[mid+1:]) if mid < len(arr)-1 else None )
    return root

class Solution:
    def balanceBST(self, root: TreeNode) -> TreeNode:
        arr = []
        store_to_array(root, arr)
        arr.sort()
        print(arr)
        return build_a_tree(arr)

​Problem: N-Ary Tree pre-order traversal

​leetcode.com/problems/n-ary-tree-preorder-traversal/

Given an n-ary tree, return the preorder traversal of its nodes' values.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

 

Follow up:

Recursive solution is trivial, could you do it iteratively?

 

Example 1:

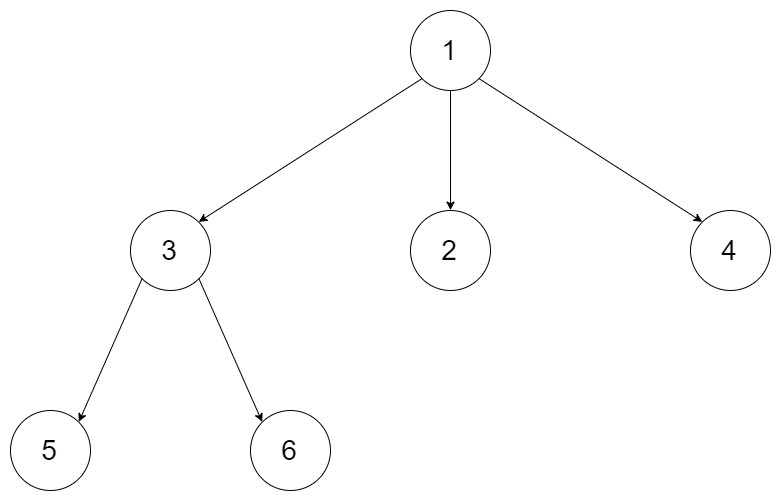
Input: root = [1,null,3,2,4,null,5,6]
Output: [1,3,5,6,2,4]

Example 2:

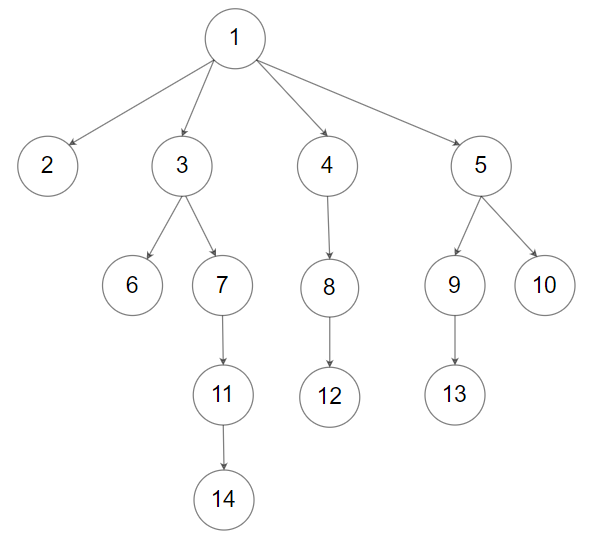
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [1,2,3,6,7,11,14,4,8,12,5,9,13,10]

 

Constraints:

• The height of the n-ary tree is less than or equal to 1000
• The total number of nodes is between [0, 10^4]

​SOLUTION:

"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""
def traverse(root, arr):
    if root == None:
        return
    if root.children == None:
        return
    for c in root.children:
        arr.append(c.val)
        traverse(c, arr)
        
class Solution:
    def preorder(self, root: 'Node') -> List[int]:
        if root == None:
            return[]
        arr = [root.val]
        traverse(root, arr)
        return arr