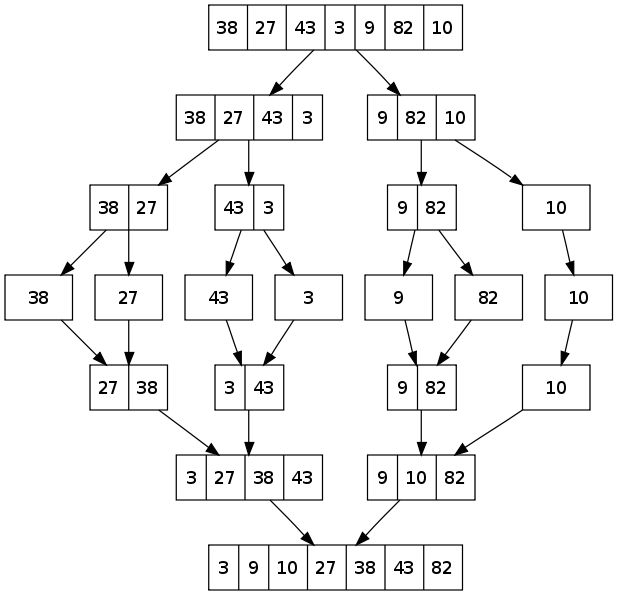
Merge Sort Implementation using Python

If you would like to practice against unit tests: https://leetcode.com/problems/sort-an-array/

• Divide by the middle until the length of the array is 1 (recursive call on the left and right sides of the array)
• Combine the array back by walking from left to right of both "left" and "right" subarrays (i, j walkers) and put smaller of the two elements into the resulting array
• Once the merge of the two arrays is complete, there may be leftover items in either "left" or the "right", we will know that if the walkers (i,j) are still smaller than the length-1 of the array, so we just copy them over if that's the case

def merge_sort(nums):
    if len(nums) <=1:
        return nums
    
    mid = len(nums) // 2
    
    left = nums[:mid]
    right = nums[mid:]
    
    merge_sort(left)
    merge_sort(right)
    
    i = j = k = 0
    
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            nums[k] = left[i]
            i+=1
        else:
            nums[k] = right[j]
            j+=1
        k+=1
        
    while i < len(left):
        nums[k] = left[i]
        i+=1
        k+=1
        
    while j < len(right):
        nums[k] = right[j]
        j+=1
        k+=1
        
    return nums

class Solution:
    def sortArray(self, nums: List[int]) -> List[int]:
        return merge_sort(nums)

Problem: Median of two sorted arrays

​leetcode.com/problems/median-of-two-sorted-arrays/

Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays.

Follow up: The overall run time complexity should be O(log (m+n)).

 

Example 1:

Input: nums1 = [1,3], nums2 = [2]
Output: 2.00000
Explanation: merged array = [1,2,3] and median is 2.

Example 2:

Input: nums1 = [1,2], nums2 = [3,4]
Output: 2.50000
Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.

Example 3:

Input: nums1 = [0,0], nums2 = [0,0]
Output: 0.00000

Example 4:

Input: nums1 = [], nums2 = [1]
Output: 1.00000

Example 5:

Input: nums1 = [2], nums2 = []
Output: 2.00000

 

Constraints:

• nums1.length == m
• nums2.length == n
• 0 <= m <= 1000
• 0 <= n <= 1000
• 1 <= m + n <= 2000
• -106 <= nums1[i], nums2[i] <= 106

SOLUTION:
​use merge sort technique

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        i = j = 0
        merged = []
        while i<len(nums1) and j<len(nums2):
            if nums1[i] < nums2[j]:
                merged.append(nums1[i])
                i+=1
            else:
                merged.append(nums2[j])
                j+=1
        while i<len(nums1):
            merged.append(nums1[i])
            i+=1
        while j<len(nums2):
            merged.append(nums2[j])
            j+=1
        #median is calculatd as:
        #if odd number of elements, then return middle element
        #if even number of elements, average the two middle ones
        return merged[len(merged)//2] if len(merged)%2==1 else\
               (merged[len(merged)//2]+merged[len(merged)//2-1])/2