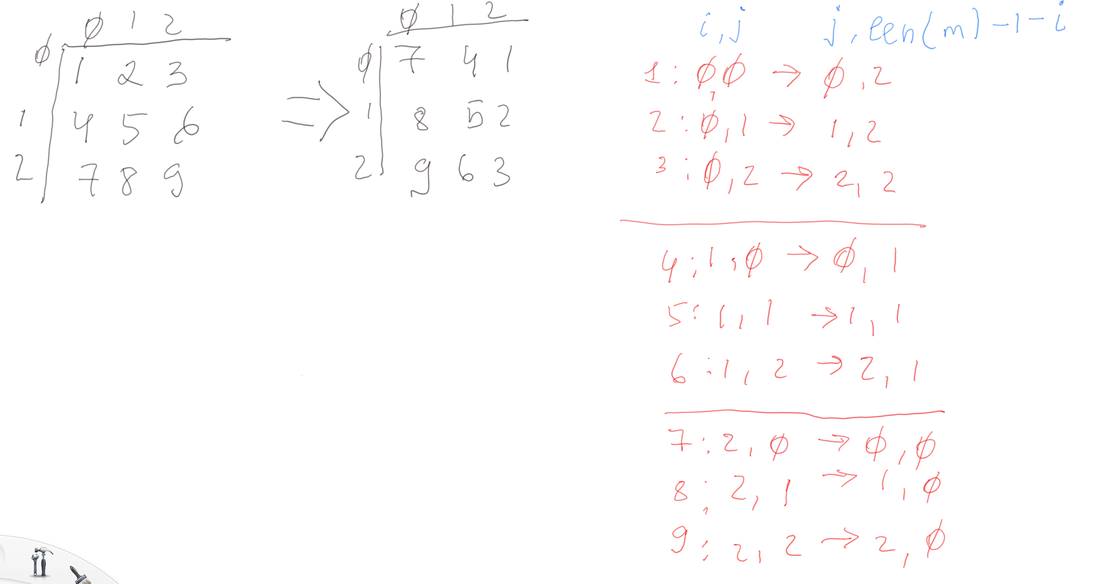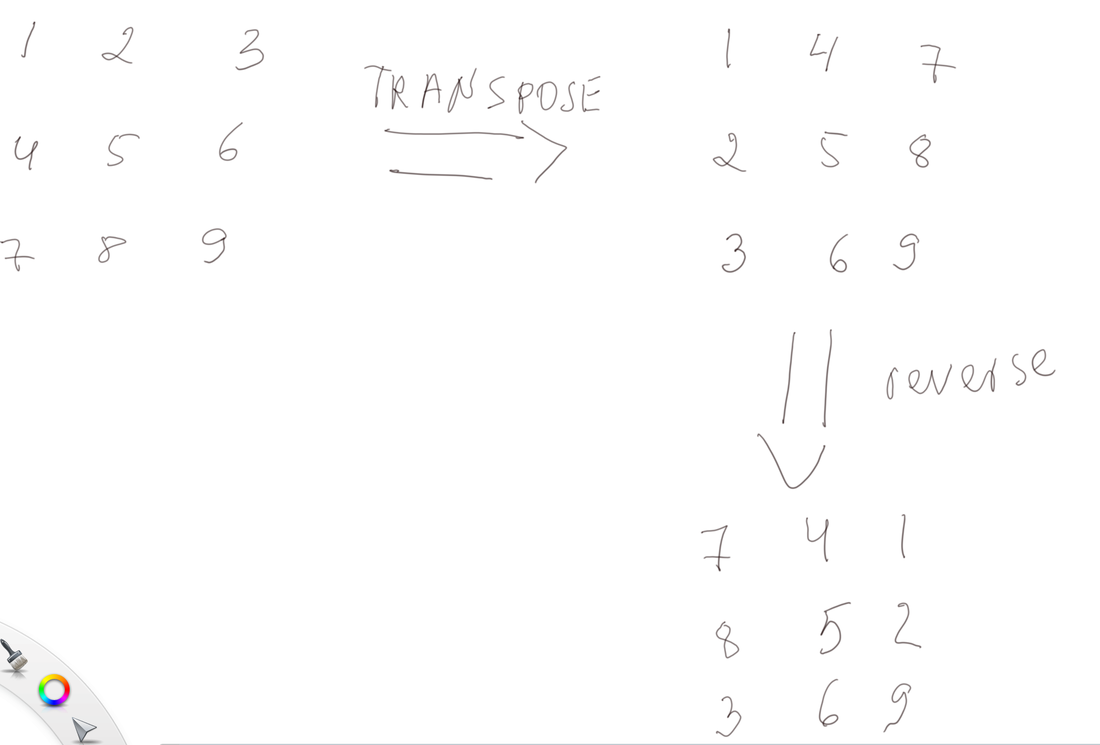Problem #1 Palindrome Permutation
leetcode.com/problems/palindrome-permutation/
leetcode.com/problems/palindrome-permutation/
Given a string, determine if a permutation of the string could form a palindrome.
Example 1:
Input: "code"
Output: false
Example 2:
Input: "aab"
Output: true
Example 3:
Input: "carerac"
Output: true
SOLUTION:
A trick to solving this problem could be counting recurrence of same characters and if we find more than one odd number of recurrences then the string cannot be turned into a palindrome
class Solution: def canPermutePalindrome(self, s: str) -> bool: dict = {}#dictionary to hold the counts for i in range(0, len(s)): dict[s[i]] = dict[s[i]] +1 if (s[i] in dict) else 1 #if we have more than one count that is odd, then #the string permutation cannot be turned into a palindrome odds = 0 for v in dict.values(): odds+=v%2 return odds <= 1
Introducing the collections module and the Counter class, please see the example below
>>> import collections >>> collections.Counter("abba") Counter({'a': 2, 'b': 2})
Same program with the Counter:
import collections class Solution: def canPermutePalindrome(self, s: str) -> bool: dict = collections.Counter(s)#dictionary to hold the counts #if we have more than one count that is odd, then #the string permutation cannot be turned into a palindrome odds = 0 for v in dict.values(): odds+=v%2 return odds <= 1
Introducing functools reduce:
reduce(function, iterable, initializer=None)
the above loop calculating odds could be re-written as in the example below
>>> import collections >>> import functools >>> >>> dict = collections.Counter("abba") >>> dict Counter({'a': 2, 'b': 2}) >>> functools.reduce(lambda odds,v: odds + v%2, dict.values(),0) 0 >>> >>> dict = collections.Counter("abcba") >>> dict Counter({'a': 2, 'b': 2, 'c': 1}) >>> functools.reduce(lambda odds,v: odds + v%2, dict.values(),0) 1 >>> >>> dict = collections.Counter("abcfba") >>> dict Counter({'a': 2, 'b': 2, 'c': 1, 'f': 1}) >>> functools.reduce(lambda odds,v: odds + v%2, dict.values(),0) 2
Now replacing the odds validation with the reduce method:
import collections import functools class Solution: def canPermutePalindrome(self, s: str) -> bool: dict = collections.Counter(s)#dictionary to hold the counts #if we have more than one count that is odd, then #the string permutation cannot be turned into a palindrome odds = functools.reduce(lambda odds,v: odds + v%2, dict.values(),0) return odds <= 1
Finally you could reduce it all to a single line, but I'd rather you not do this, as the code becomes very difficult to read
import collections import functools class Solution: def canPermutePalindrome(self, s: str) -> bool: return functools.reduce(lambda odds,v: odds + v%2, collections.Counter(s).values(),0) <= 1
We are given two strings, A and B.
A shift on A consists of taking string A and moving the leftmost character to the rightmost position. For example, if A = 'abcde', then it will be 'bcdea' after one shift on A. Return True if and only if A can become B after some number of shifts on A.
Example 1: Input: A = 'abcde', B = 'cdeab' Output: true Example 2: Input: A = 'abcde', B = 'abced' Output: false
Note:
AandBwill have length at most100.
SOLUTION:
- Note that index function throws an exception if substring is not found
- if the lengths of the two strings don't match, then return False off the bat
- A+A creates all possible combinations of the rotation of the A string and if B is present as a substring in that rotation, return True
class Solution: def rotateString(self, A: str, B: str) -> bool: if len(A) != len(B): return False res = 1 try: (A+A).index(B) except: res = 0 return bool(res)
You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
Example 1:
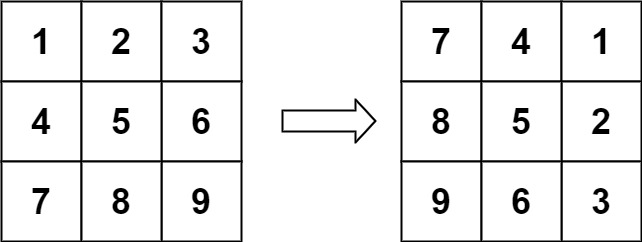
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]] Output: [[7,4,1],[8,5,2],[9,6,3]]
Example 2:
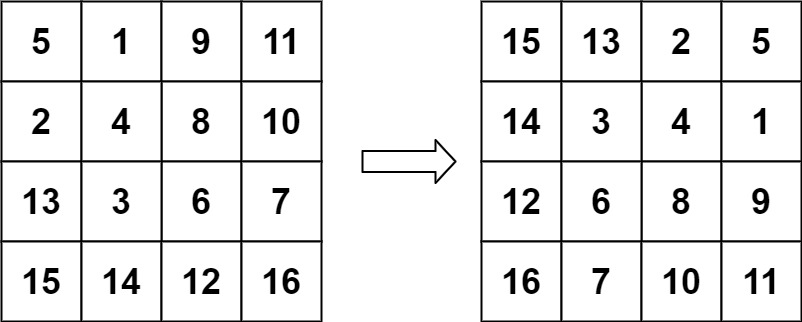
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
Example 3:
Input: matrix = [[1]] Output: [[1]]
Example 4:
Input: matrix = [[1,2],[3,4]] Output: [[3,1],[4,2]]
Constraints:
matrix.length == nmatrix[i].length == n1 <= n <= 20-1000 <= matrix[i][j] <= 1000
SOLUTION:
First, we will try to solve it not in place
matrix = [[1,2,3],[4,5,6],[7,8,9]] n = len(matrix) new_matrix = [[0]*n for i in range(n)] for i in range(0,n): for j in range(0,n): new_matrix[j][n-1-i] = matrix[i][j] print(new_matrix) #prints [[7, 4, 1], [8, 5, 2], [9, 6, 3]]
easy-peasy...
Now, let's think about the in-place rotation.
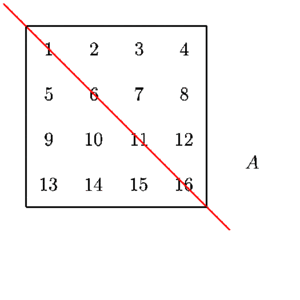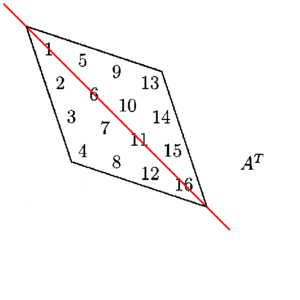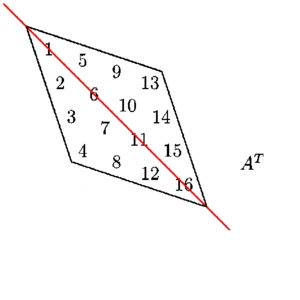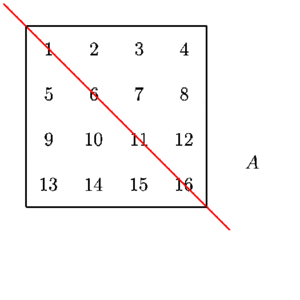
There is a Matrix transposition in place algorithm that is pretty easy to remember, it lets you flip the matrix rows and columns and the only thing you need to remember is that you have to flip by diagonal (half the matrix), otherwise you will copy everything back to its place.
this is what may come to mind intuitively:
Now, let's think about the in-place rotation.
There is a Matrix transposition in place algorithm that is pretty easy to remember, it lets you flip the matrix rows and columns and the only thing you need to remember is that you have to flip by diagonal (half the matrix), otherwise you will copy everything back to its place.
this is what may come to mind intuitively:
for i in range(0,n): for j in range(0,n): matrix[i][j], matrix[j][i] =\ matrix[j][i], matrix[i][j]
and the correction point to make it flip by the diagonal would be (note the i on the line 2):
1 2 3 4 | for i in range(0,n): for j in range(i,n): matrix[i][j], matrix[j][i] =\ matrix[j][i], matrix[i][j] |
Now that we can transpose the matrix in place and we look at what we get as a result, you san see that the rotation of the matrix is equal to it's transposition plus the reverse:
there is a reverse array function in python that reverses the array in place (if there wasn't we would go from the two ends of the array inward flipping the numbers in place)
>>> arr = [1,2,3,4,5,6] >>> arr.reverse() >>> arr [6, 5, 4, 3, 2, 1]
And your final result would look like this:
class Solution: def rotate(self, matrix: List[List[int]]) -> None: """ Do not return anything, modify matrix in-place instead. """ n = len(matrix) for i in range(0,n): for j in range(i,n): matrix[i][j], matrix[j][i] =\ matrix[j][i], matrix[i][j] for i in range(0, n): matrix[i].reverse()